Gerbang logika atau
gerbang logik adalah suatu entitas dalam
elektronika dan
matematika Boolean
yang mengubah satu atau beberapa masukan logik menjadi sebuah sinyal
keluaran logik. Gerbang logika terutama diimplementasikan secara
elektronis menggunakan
diode atau
transistor, akan tetapi dapat pula dibangun menggunakan susunan komponen-komponen yang memanfaatkan sifat-sifat
elektromagnetik (
relay),
cairan,
optik dan bahkan
mekanik.
Gerbang elektronika
Untuk membangun sistem logika yang berfungsi secara penuh,
relay, tabung hampa, atau
transistor dapat digunakan. Contoh gerbang logika yaitu
logika resistor-transistor (
resistor-transistor logic / RTL),
logika diode–transistor (
diode-transistor logic / DTL),
logika transistor-transistor (
transistor-transistor logic / TTL), dan logika
complementary metal–oxide–semiconductor (
CMOS).
Jenis-jenis gerbang logika
| Nama |
Fungsi |
Lambang dalam rangkaian |
Tabel kebenaran |
| IEC 60617-12 |
US-Norm |
DIN 40700 (sebelum 1976) |
Gerbang-AND
(AND) |


 |
 |
 |
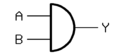 |
| A |
B |
Y |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
|
Gerbang-OR
(OR) |

 |
 |
 |
 |
| A |
B |
Y |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
|
Gerbang-NOT
(NOT, Gerbang-komplemen, Pembalik(Inverter)) |

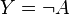 |
 |
 |
 |
\
|
Gerbang-NAND
(Not-AND) |


 |
 |
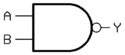 |
 |
| A |
B |
Y |
| 0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
|
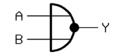
Gerbang-NOR
(Not-OR) |
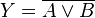

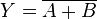 |
 |
 |
 |
| A |
B |
Y |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
|
Gerbang-XOR
(Antivalen, Exclusive-OR) |
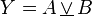
 |
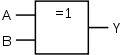 |
 |

atau
 |
| A |
B |
Y |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
|
Gerbang-XNOR
(Ekuivalen, Not-Exclusive-OR) |
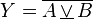

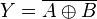 |
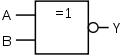 |
 |

atau
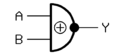 |
| A |
B |
Y |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
|
Tabel Kebenaran
Tabel kebenaran
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Dalam
logika matematika,
tabel kebenaran adalah tabel dalam
matematika
yang digunakan untuk melihat nilai kebenaran dari suatu
premis/pernyataan. Jika hasil akhir adalah benar semua (dilambangkan B,
T, atau 1), maka disebut
tautologi. Sedangkan jika salah semua (S, F, atau 0) disebut
kontradiksi. Premis yang hasil akhirnya gabungan benar dan salah disebut
kontingensi.
Operasi Binary
Tabel kebenaran untuk semua logikal operasi binary
| P |
Q |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| T |
T |
|
F |
F |
F |
F |
F |
F |
F |
F |
|
T |
T |
T |
T |
T |
T |
T |
T |
| T |
F |
|
F |
F |
F |
F |
T |
T |
T |
T |
|
F |
F |
F |
F |
T |
T |
T |
T |
| F |
T |
|
F |
F |
T |
T |
F |
F |
T |
T |
|
F |
F |
T |
T |
F |
F |
T |
T |
| F |
F |
|
F |
T |
F |
T |
F |
T |
F |
T |
|
F |
T |
F |
T |
F |
T |
F |
T |
dimana T = benar and F = salah.
Kunci:
Logical operators can also be visualized using
Venn diagrams.
Jenis-jenis operasi pada tabel kebenaran
Operasi yang digunakan adalah
- Negasi
Tabel kebenaran untuk
TIDAK p (juga ditulis
¬p,
Np,
Fpq, or
~p) adalah dibawah ini:
Logika negasi
| p |
¬p |
| S |
B |
| B |
S |
- Konjungsi
Tabel kebenaran untuk
p DAN q (juga ditulis
p ∧ q,
Kpq,
p & q, atau
p  q
q) adalah dibawah ini:
Logika konjungsi
| p |
q |
p ∧ q |
| B |
B |
B |
| B |
S |
S |
| S |
B |
S |
| S |
S |
s |
- Disjungsi inklusif (sering disebut sebagai disjungsi saja)
Tabel kebenaran untuk
p ATAU q (juga ditulis
p ∨ q,
Apq,
p || q, or
p + q) adalah dibawah ini:
Logika Disjungsi
| p |
q |
p ∨ q |
| B |
B |
B |
| B |
S |
B |
| S |
B |
B |
| S |
S |
S |
- Kesamaan
Tabel kebenaran untuk
p XNOR q (juga ditulis
p ↔ q,
Epq,
p = q, or
p ≡ q) adalah dibawah ini:
Logika kesamaan
| p |
q |
p ≡ q |
| B |
B |
B |
| B |
S |
S |
| S |
B |
S |
| S |
S |
B |
- Disjungsi eksklusif
Tabel kebenaran untuk
p XOR q (juga ditulis
p ⊕ q,
Jpq, or
p ≠ q) adalah dibawah ini:
Disjungsi eksklusif
| p |
q |
p ⊕ q |
| B |
B |
S |
| B |
S |
B |
| S |
B |
B |
| S |
S |
S |
- Implikasi
- Biimplikasi
Jumlah kemungkinan hasil adalah

, dimana n adalah jumlah pernyataan dasar yang ada (p, q, r, dsb). Namun, p dan ~p (
negasi p) tidak dihitung sebagai pernyataan yang berbeda.











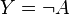









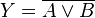

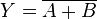



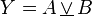

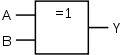



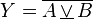

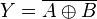
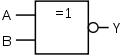



 q) adalah dibawah ini:
q) adalah dibawah ini: , dimana n adalah jumlah pernyataan dasar yang ada (p, q, r, dsb). Namun, p dan ~p (negasi p) tidak dihitung sebagai pernyataan yang berbeda.
, dimana n adalah jumlah pernyataan dasar yang ada (p, q, r, dsb). Namun, p dan ~p (negasi p) tidak dihitung sebagai pernyataan yang berbeda.
Tidak ada komentar:
Posting Komentar